排序算法
插入排序
原理
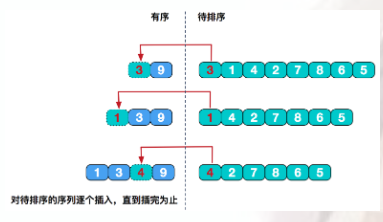
算法原理:从整个待排序列中选出一个元素插入到已经有序的子序列中去,得到一个有序的、元素加一的子序列,直到整个序列的待插入元素为0,则整个序列全部有序。
具体的实现的时候,我们一般选择第一个元素作为有序的序列,将后面的元素插入到前面有序的序列直到整个序列有序。
时间复杂度:插入排序在最好情况下,需要比较n-1次,无需交换元素,时间复杂度为O(n);在最坏情况下,时间复杂度为O(n^2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| #include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int len=15;
int main()
{
int a[len]={1,87,64,19,53,14,57,62,23,37,48,9,91,45,81};
for(int i=1;i<len;i++)
{
int j=i;
int temp=a[i];
while(j>0)
{
if(a[j-1]<a[i])
{
for(int k=i;k>j;k--)
a[k]=a[k-1];
a[j]=temp;
break;
}
j--;
}
}
for(int i=0;i<len;i++)
printf("%d ",a[i]);
printf("\n");
return 0;
}
|
选择排序
原理
算法原理:为每一趟从待排序的数据元素中选择最小(或最大)的一个元素作为首元素,直到所有元素排完为止
算法步骤:
- 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
- 再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
- 重复第二步,直到所有元素均排序完毕。
时间复杂度:无论数组原始排列如何,比较次数是不变的;对于交换操作,在最好情况下也就是数组完全有序的时候,无需任何交换移动,
在最差情况下,也就是数组倒序的时候,交换次数为n-1次。综合下来,时间复杂度为O(n^2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| #include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int len=15;
int main()
{
int a[len]={1,87,64,19,53,14,57,62,23,37,48,9,91,45,81};
for(int i=0;i<len-1;i++)
{
int temp=i;
for(int j=i+1;j<len;j++)
{
if(a[temp]>a[j])
temp=j;
}
if(temp!=i)
swap(a[temp],a[i]);
}
for(int i=0;i<len;i++)
printf("%d ",a[i]);
printf("\n");
return 0;
}
|
冒泡排序
原理
算法原理:比较相邻的元素。如果第一个比第二个大,就交换他们两个
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
时间复杂度分析:最优时间O(n),最差时间O(n^2)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| #include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int len=15;
int main()
{
int a[len]={1,87,64,19,53,14,57,62,23,37,48,9,91,45,81};
for(int i=0;i<len-1;i++)
{
bool flag=false;
for(int j=0;j<len-1-i;j++)
{
if(a[j]>a[j+1])
{
swap(a[j],a[j+1]);
flag=true;
}
}
if(flag==false)
break;
}
for(int i=0;i<len;i++)
printf("%d ",a[i]);
printf("\n");
return 0;
}
|
归并排序
原理
算法原理:是利用递归与分治的技术将数据序列划分为越来越小的半子表,再对半子表排序,最后再用递归方法将排好序的半子表合并成越来越大的有序序列。
时间复杂度:O(nlogn)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| #include <iostream>
#include <cstdio>
using namespace std;
int a[20]={5,6,9,15,4,-1,-9,5,-6,71,5,-36,2,15,48,-15,14,6,9,11};
int l,r;
void mergee(int l,int m,int r)
{
int T[20];
int i=l,j=m+1;
int k=0;
while(i<=m&&j<=r)
{
if(a[i]<=a[j])
T[k++]=a[i++];
else
T[k++]=a[j++];
}
while(i<=m)
T[k++]=a[i++];
while(j<=r)
T[k++]=a[j++];
for(int i=0;i<k;i++)
a[l+i]=T[i];
}
int mergr_sort(int l,int r)
{
if(r-l>0)
{
int mid=(l+r)/2;
int p=l,q=mid,i=l;
mergr_sort(l,mid);
mergr_sort(mid+1,r);
mergee(l,mid,r);
}
}
int main()
{
scanf("%d %d",&l,&r);
mergr_sort(l,r);
for(int i=0;i<20;i++)
printf("%d ",a[i]);
printf("\n");
return 0;
}
|
快速排序
原理
通过一轮的排序将序列分割成独立的两部分,其中一部分序列的关键字(这里主要用值来表示)均比另一部分关键字小。继续递归的对长度较短的序列进行同样的分割,最后到达整体有序。为了实现一次划分,我们可以从数组(假定数据是存在数组中)的两端移动下标,必要时交换记录,直到数组两端的下标相遇为止。为此,我们附设两个指针(下角标)i和j, 通过j 从当前序列的有段向左扫描,越过不小于基准值的记录。当遇到小于基准值的记录时,扫描停止。通过i从当前序列的左端向右扫描,越过小于基准值的记录。当遇到不小于基准值的记录时,扫描停止。交换两个方向扫描停止的记录 a[j] 与 a[i]。 然后,继续扫描,直至 i与j 相遇为止。它的平均时间复杂度为O(nlogn)。
当我们每次进行分区划分时,如果每次选择的基准元素都是当前序列中最大或最小的记录,这样每次分区的时候只得到了一个新分区,另一个分区为空,并且新分区只是比分区前少一个元素,这是快速排序的最坏情况,时间复杂度上升为O(n^2)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| #include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int len=15;
int a[len]={1,87,64,19,53,14,57,62,23,37,48,9,91,45,81};
void quicksort(int l,int r)
{
if(l>r)
return;
int temp=a[l];
int i=l;int j=r;
while(i!=j)
{
while(a[j]>=temp&&i<j)
j--;
while(a[i]<=temp&&i<j)
i++;
if(i<j)
swap(a[i],a[j]);
}
a[l]=a[i];
a[i]=temp;
quicksort(l,i-1);
quicksort(i+1,r);
}
int main()
{
quicksort(0,14);
for(int i=0;i<len;i++)
printf("%d ",a[i]);
printf("\n");
return 0;
}
|
堆排序
原理
利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。
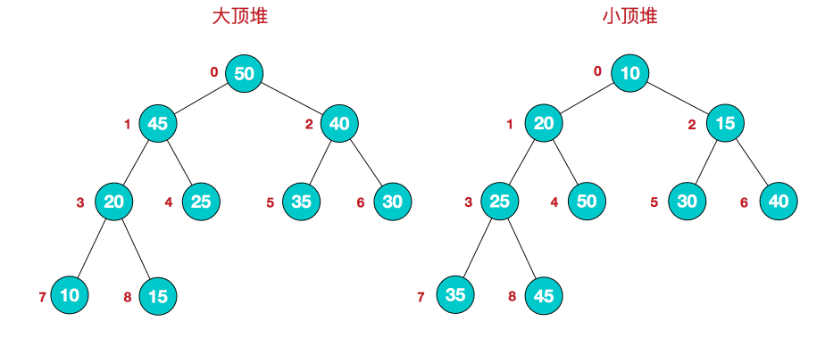
该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
算法步骤:
- 将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
- 将堆顶元素与末尾元素交换,将最大元素”沉”到数组末端;
- 重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| package sortdemo;
import java.util.Arrays;
public class HeapSort {
public static void main(String []args){
int []arr = {9,8,7,6,5,4,3,2,1};
sort(arr);
System.out.println(Arrays.toString(arr));
}
public static void sort(int []arr){
for(int i=arr.length/2-1;i>=0;i--){
adjustHeap(arr,i,arr.length);
}
for(int j=arr.length-1;j>0;j--){
swap(arr,0,j);
adjustHeap(arr,0,j);
}
}
public static void adjustHeap(int []arr,int i,int length){
int temp = arr[i];
for(int k=i*2+1;k<length;k=k*2+1){
if(k+1<length && arr[k]<arr[k+1]){
k++;
}
if(arr[k] >temp){
arr[i] = arr[k];
i = k;
}else{
break;
}
}
arr[i] = temp;
}
public static void swap(int []arr,int a ,int b){
int temp=arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}
|
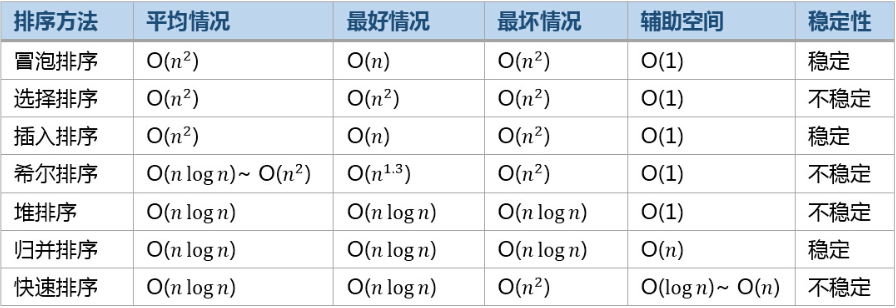
几种排序算法的比较示意图
排序稳定性的定义
通俗地讲就是能保证排序前两个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。在简单形式化一下,如果Ai = Aj,Ai原来在位置前,排序后Ai还是要在Aj位置前
二叉平衡树
左右子树的的高度差不超过1, 否则要进行树的调整
二叉查找树
1, 左子树上所有的节点的值均小于或等于他的根节点的值
2, 右子数上所有的节点的值均大于或等于他的根节点的值
3, 左右子树也一定分别为二叉排序树
传统的查找树的缺点: 如果树太高就会导致查找效率低下, 接近线性查找的时间复杂度
红黑树
红黑树就是一种平衡的二叉查找树,说他平衡的意思是他不会变成“瘸子”,左腿特别长或者右腿特别长。除了符合二叉查找树的特性之外,还具体下列的特性:
- \1. 节点是红色或者黑色
- \2. 根节点是黑色
- \3. 每个叶子的节点都是黑色的空节点(NULL)
- \4. 每个红色节点的两个子节点都是黑色的。
- \5. 从任意节点到其每个叶子的所有路径都包含相同的黑色节点。





